-

Фотка Машины тьюринга в jpg -

Фотка Машины тьюринга для загрузки -

Картинка Машины тьюринга для скачивания в jpg -

Изображение Машины тьюринга в png -

Фото Машины тьюринга в формате jpg -

Изображение Машины тьюринга в формате png -

Фотография Машины тьюринга в png -

Фотка Машины тьюринга для загрузки -

Изображение Машины тьюринга в формате png -

Фотография Машины тьюринга в формате png -

Картинка Машины тьюринга в формате webp -

Фотография Машины тьюринга в формате png -

Фотография Машины тьюринга в jpg -

Фото Машины тьюринга для скачивания в webp -

Изображение Машины тьюринга в формате jpg -
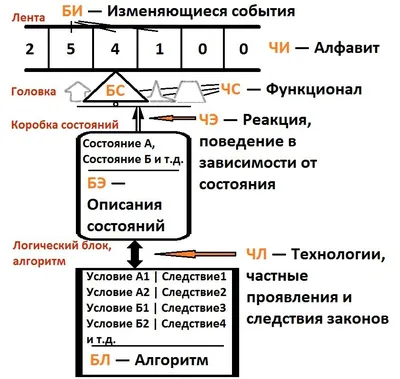
Фото Машины тьюринга на выбор -
Фото Машины тьюринга для загрузки в png -
Фотка Машины тьюринга в формате png -
Фотография Машины тьюринга в png -

Фото Машины тьюринга для скачивания в webp -

Фото Машины тьюринга на выбор -
Изображение Машины тьюринга в формате jpg -

Фото Машины тьюринга для загрузки в webp -

Фото Машины тьюринга на выбор -

Фотография Машины тьюринга в формате webp -

Фотография Машины тьюринга в jpg -

Фотография Машины тьюринга в jpg -
Фото Машины тьюринга для загрузки в jpg -

Изображение Машины тьюринга в формате png -

Фотка Машины тьюринга в png -

Картинка Машины тьюринга в формате webp -

Картинка Машины тьюринга в формате webp -

Изображение Машины тьюринга в формате png -

Фотография Машины тьюринга в jpg -

Фотка Машины тьюринга в jpg -

Фото Машины тьюринга для загрузки в png -
Фотка Машины тьюринга для скачивания
Машина Тьюринга
Машина Тьюринга - это абстрактное устройство, предложенное английским математиком Аланом Тьюрингом в 1936 году. Она является универсальной вычислительной моделью, способной выполнить любой алгоритм, который может быть выражен как последовательность простых инструкций.
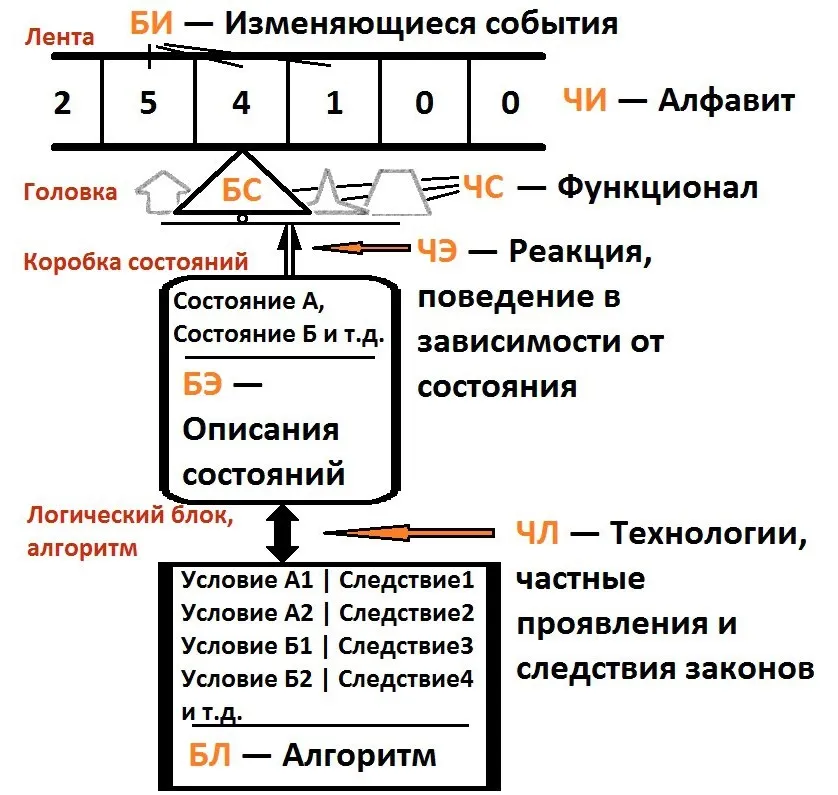
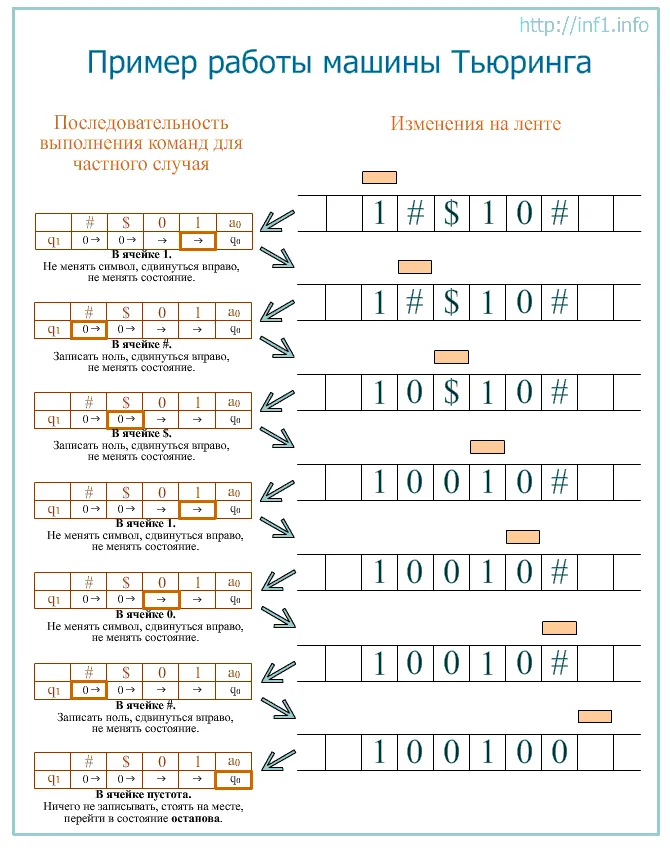
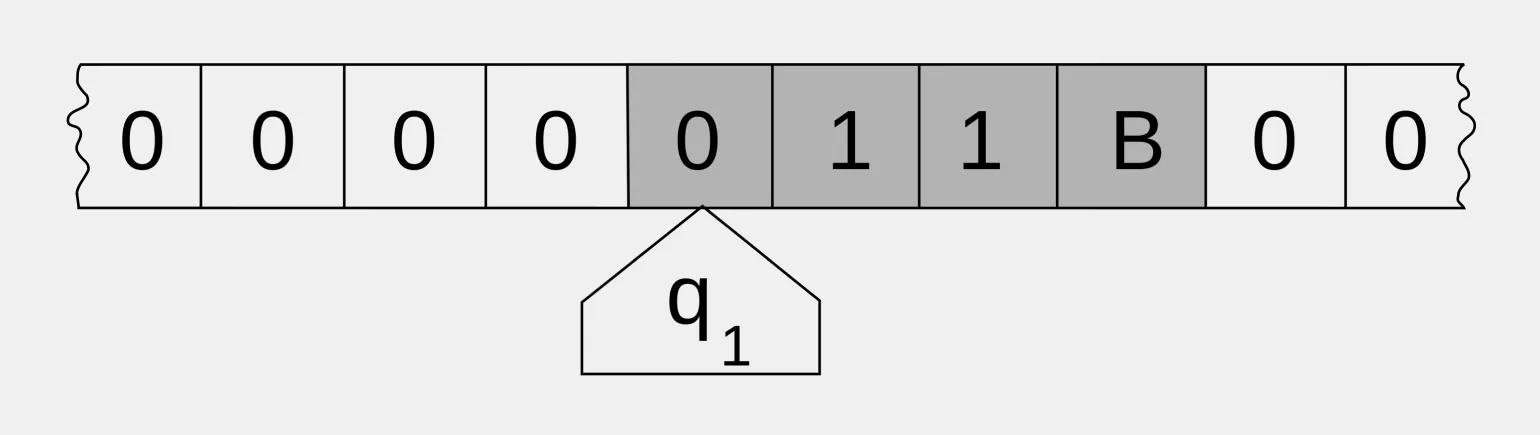
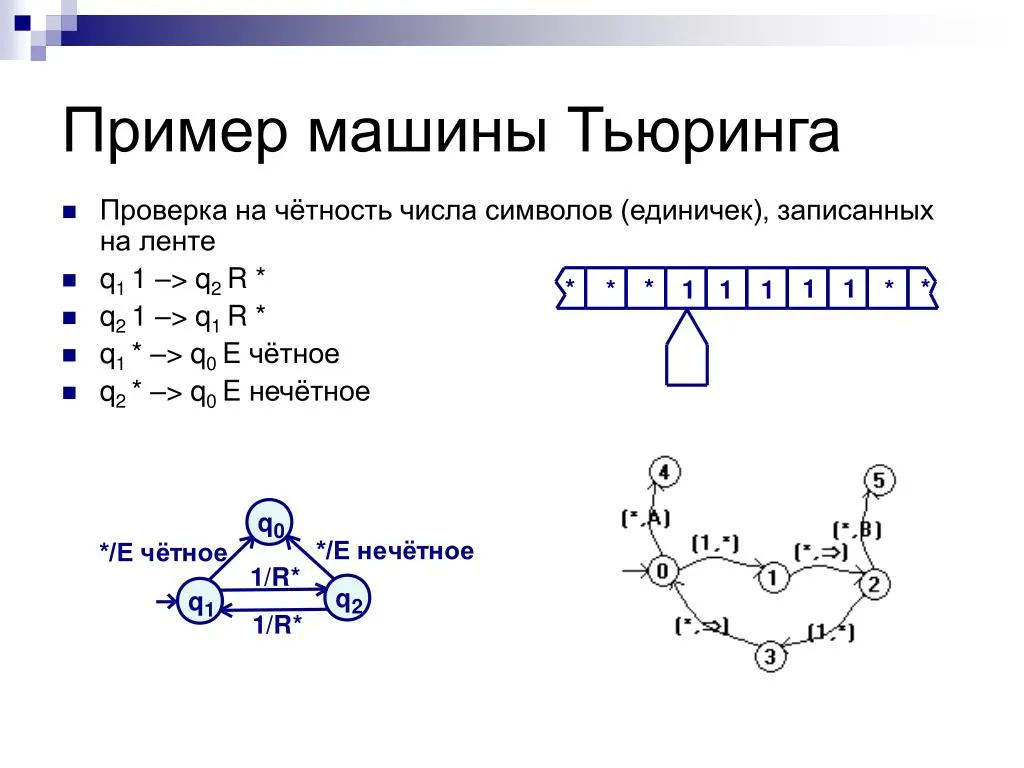
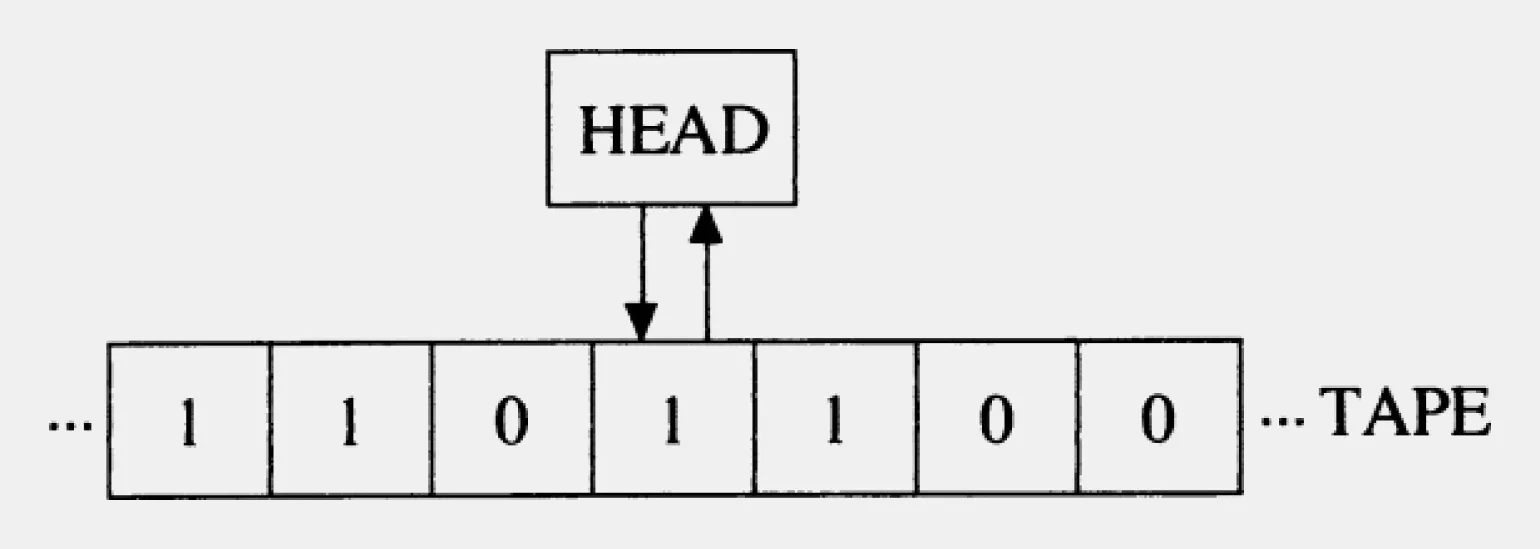
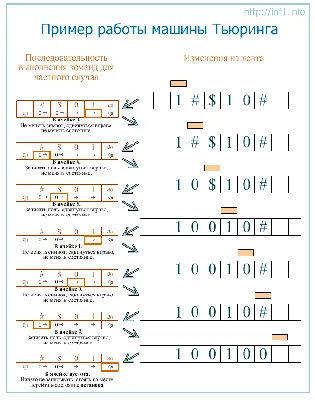
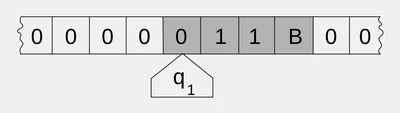
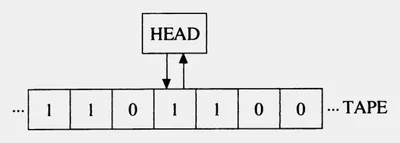
Машина Тьюринга состоит из бесконечной ленты, на которой располагаются ячейки для записи символов, и головки, которая может передвигаться вдоль этой ленты и считывать или записывать символы. В зависимости от состояния, в котором находится машина, головка выполняет определенную операцию - сдвиг влево или вправо, запись символа, считывание символа или переход в другое состояние.
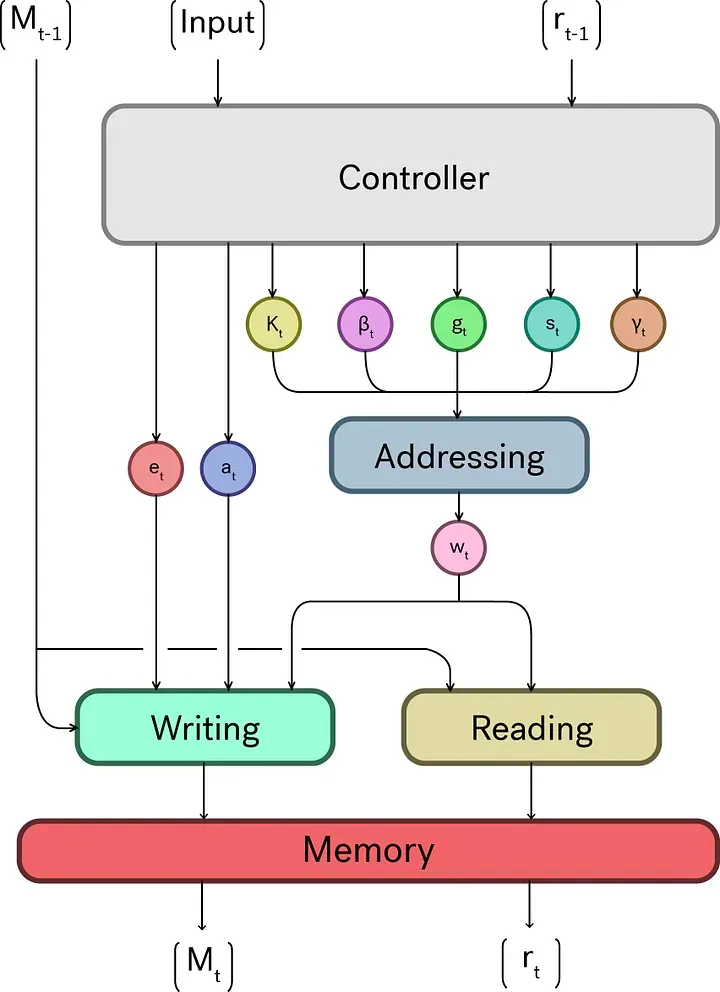
Основная идея машины Тьюринга заключается в том, что она может имитировать работу любого другого вычислительного устройства. Путем представления данных в виде символов на ленте, и управления головкой с помощью конечного числа состояний и правил перехода, машина Тьюринга способна выполнять любые вычисления.
Не смотря на свою простоту и абстрактность, машина Тьюринга обладает удивительной вычислительной мощностью. Она может решать различные задачи, включая выполнение арифметических операций, решение логических задач, обработку строк и многое другое. Более того, существует связь между машиной Тьюринга и понятием вычислимости, которая помогла сформулировать теорию вычислительности и понять пределы возможных вычислений.
Машины Тьюринга имеют широкое применение в теории алгоритмов и теоретической информатике. Они используются для исследования сложности вычислений, разработки и доказательства алгоритмов, а также анализа теоретических пределов возможных вычислений. Кроме того, машина Тьюринга является ключевым понятием в области искусственного интеллекта и теории автоматического доказательства.
В заключение, машина Тьюринга - это абстрактное устройство, которое является универсальным вычислительным устройством. Она представляет собой модель, способную выполнить любой алгоритм и имеет широкое применение в теории алгоритмов и теоретической информатике. Машина Тьюринга играет важную роль в исследовании вычислимости и помогает нам лучше понять границы возможных вычислений.